Iron ore normative mineralogy
- 6 minutes read - 1115 words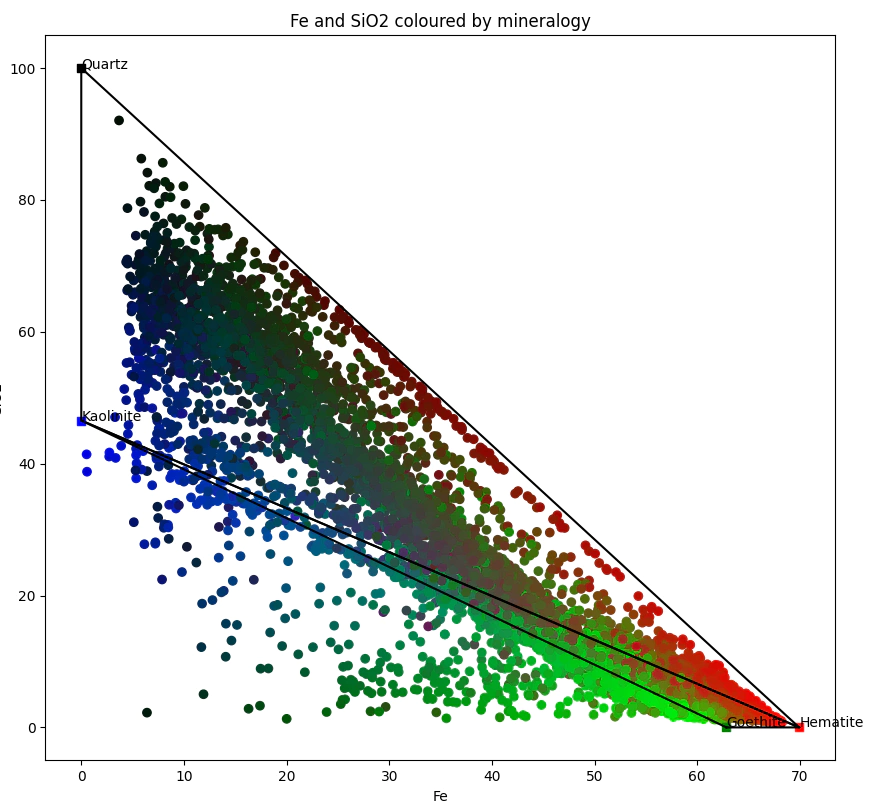
Assays are not always able to provide all the information that we need for a geological problem.
On occasion we might need to know the mineralogical density of a sample to estimate porosity or some other physical property of the minerals themselves.
Normative mineralogy is a cheap solution to these problems if you know how to do it.
In this post I will demonstrate how to calculate a limited but useful set of minerals from assay for iron ore similar methods can be used for other deposit types too.
As usual we are using open file data in this case the 2014 Roy Hill Annual Report
Let’s first install the required packages:
pip install git+https://github.com/FractalGeoAnalytics/AuGeoscienceDataSets
pip install matplotlib numpy pandas
Once we have the required packages we are going to download the required zip file of geological data.
from pathlib import Path
import shutil
import numpy as np
from augeosciencedatasets import downloaders
from augeosciencedatasets import readers
import pandas as pd
from matplotlib import pyplot as plt
# download the drilling data from DASC
outpath = Path('data/royhill')
if not outpath.exists():
outpath.mkdir(parents=True)
dasc_url = "https://geodocsget.dmirs.wa.gov.au/api/GeoDocsGet?filekey=4176a02b-1d7e-49fd-b725-36427e646200-zkectqkylt37561ucrzskmj5nsri06i9nff0jrkt"
outfile = outpath.joinpath('A101166_Drilling_13339409.zip')
downloaders.from_dasc(dasc_url,outfile)
# unzip the zip file
shutil.unpack_archive(outfile,outpath)
Now we load the data, using the WADG3 file reader it doesn’t convert the numbers to float so we will convert those.
The data is missing the Al2O3 assay for unknown reasons, but we won’t let that get in the way of estimating a Kaolinite content.
# THE " " in the file name is deliberate
assay_path = outpath.joinpath('RH_WADG3_ASS2014 .txt')
assay,_ = readers.dmp(assay_path)
# functions that cleans up the dmp formatted data into something useful
# first map the objects to floats
def map_float(x):
try:
y = float(x)
except:
y = np.nan
return y
# function to remove the extra information of lab codes and units
def clean_columns(x):
return x.replace('_XRF78L_pct','').replace('_WGH79_g','').replace('_CSA06V_pct','')
# remove the extra information in the columns.
assay.columns = assay.columns.map(clean_columns)
# select the elements that we need to solve for Goethite, Hematite Kaolinite and Quartz
# N.B Al2O3 is missing.
clean_ass = assay[['Fe','SiO2', 'LOI425', 'LOI650','LOI1000']]
# convert the object datatypes to float.
clean_ass = clean_ass.applymap(map_float,None).dropna()
Before we can calculate the mineralogy we are going to need create a dataset with the elemental compositions of the minerals that we are interested in solving for.
For this example we are going to use the following 4 minerals, Hematite, Goethite, Kaolinite and Quartz which for an iron ore deposit cover the majority of the minerals making up the rock mass.
I have precalculated the conversion from mineral formula to analytical weights here, please note well that the Roy Hill data is assayed with 3point TGA, which makes up for the lack of Al2O3 assay in the data. Goethite and Kaolinite can be seperated by their differential response in LOI425 and LOI650.
# here are the precalculated mineral weights in proportions
# you can do this is moles but it is more complex than required.
mineral_data = pd.DataFrame([{'Mineral':'Goethite' , 'Fe':0.6285,'SiO2':0,'LOI425':0.1013,'LOI650':0,'LOI1000':0},
{'Mineral':'Hematite','Fe':0.6994,'SiO2':0,'LOI425':0,'LOI650':0,'LOI1000':0},
{'Mineral':'Kaolinite','Fe':0 ,'SiO2':0.4654,'LOI425':0,'LOI650':0.1395,'LOI1000':0},
{'Mineral':'Quartz' , 'Fe':0 ,'SiO2':1,'LOI425':0,'LOI650':0,'LOI1000':0}])
Using the dataframe of weights we are going to run the process of calculating how much of the mineral exists in the sample. The process to calculate a normative mineralogy is made of the following 5 steps:
Divide each of the analytes in the assay table by the analyte weight in the table of minerals.
If the mineral consumes two or more analytes we limit the amount of the mineral to the limiting reagent.
We also clip the amount of the mineral to physical constraints i.e. it must lie between 1 and 0.
We then multiply the assay weights of the mineral by it’s proportion to give the amount of assay consumed by that mineral.
This is then subtracted from the assay of the sample and this residual is then used in proceeding calculations for the remaining minerals in the list.
I always find these calculations difficult to follow in text. So below is the required calculations in commented code with adjustments for efficiency.
# extract from the table of mineral compositions
# the elements for all the minerals
mineral_elements = mineral_data.columns[1:]
# extract into a matrix for easy calculation
mineral_array = mineral_data[mineral_elements].values
# create a new matrix from the dataframe of assays
# a table with the same ordering of analytes as the mineral data
cm = clean_ass[mineral_elements].values/100
# we need to create an array the same of the dimension
# n_samples x n_minerals to store the solution.
# we need the number of minerals that we are trying to solve for
n_minerals = mineral_array.shape[0]
# we need the number of samples that we need to solve for
n_assay = cm.shape[0]
# create an array of zeros this is where our result is going
mineral_solution = np.zeros((n_assay, n_minerals))
# loop over each of the rows in the mineral array
# we use enumerate as this makes it easy to keep track of the
# iteration number
for i,mineral_weights in enumerate(mineral_array):
# find the weights that are greater than 0 for the mineral
# if you don't only use the weights greater than 0
# we end up with np.inf values which is very problematic
mult_idx = mineral_weights>0
# we need to know the number of elements for later
n_elems = np.sum(mult_idx)
# step 1 divide each of the analytes in the assay table by the analyte weight in the table of minerals.
initial_product = cm[:,mult_idx]/mineral_weights[mult_idx]
# step 2 If the mineral consumes two or more analytes we limit the amount of the mineral to the limiting reagent.
mineral_lim = np.min(initial_product,1)
# step 3 We also clip the amount of the mineral to physical constraints i.e. it must lie between 1 and 0.
mineral_lim = np.clip(mineral_lim,0,1)
# step 4 We then multiply the assay weights of the mineral by it's proportion to give the amount of assay consumed by that mineral.
remaining_element = mineral_weights[mult_idx].reshape(-1,n_elems)*mineral_lim.reshape(-1,1)
# step 5 This is then subtracted from the assay of the sample and this residual is then used in proceeding calculations for the remaining minerals in the list.
cm[:,mult_idx] = cm[:,mult_idx]-remaining_element
# once we have completed all the steps place the result in our preallocated array
mineral_solution[:,i] = mineral_lim
To finish up we need to generate a sanity check plot. I like to plot Fe and SiO2. To make an image that catches the eye let’s color each of the points by their composition. Hematite as the Red channel, Kaolinite as Blue, Goehite as the Green.
For additional niceness let’s add the mineral end members and add a few mixing lines which makes the plot at the top of the post.
mineral_colors = {'Goethite':'g','Hematite':'r','Kaolinite':'b','Quartz':'k'}
plt.title('Fe and SiO2 coloured by mineralogy')
plt.scatter(clean_ass.Fe,clean_ass.SiO2, c=mineral_solution[:,[1,0,2]])
for i,mineral in mineral_data.iterrows():
plt.text(mineral.Fe*100, mineral.SiO2*100,mineral.Mineral)
plt.scatter(mineral.Fe*100, mineral.SiO2*100,marker="s",c=mineral_colors[mineral.Mineral])
plt.xlabel('Fe')
plt.ylabel('SiO2')
plt.show()